Фигуры: основные типы и их особенности

Фигуры: основные типы и их особенности

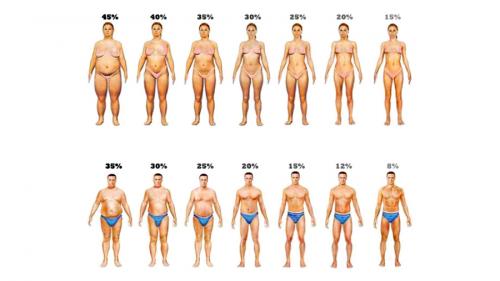
Типы телосложения — эктоморф, эндоморф и мезоморф — это идеальные образцы строения человеческого тела и модели работы его метаболизма. С этими параметрами связывают пропорции фигуры, распределение и количество жира и мышц, скорость набора и потери веса, а также эффективность тренировок. Доказательная наука в целом принимает эту классификацию.

Концепция соматотипов была разработана в 1940-х годах. Ее создал американский психолог и врач Уильям Шелдон. С тех пор ее используют фитнес-тренеры, нутрициологи и диетологи для составления индивидуальных программ тренировок и питания. Система Шелдона легла в основу теории немецкого психолога Эрнста Кречмера, в которой телосложения тоже делятся на три типа: астенический, атлетический, пикнический.

С годами теория Шелдона была довольно сильно переработана, сглажена и нюансирована. Например, изначально предполагалось, что тип фигуры невозможно изменить. Но сегодня специалисты считают, что это реально. К примеру, если эктоморф будет постоянно переедать и вести сидячий образ жизни, со временем он приобретет черты эндоморфа. «Кроме того, первоначально Шелдон считал, что размер и форма тела помогают определить такие черты личности, как напористость, агрессивность, застенчивость и чувствительность , — говорит Лиза Гильман, руководитель отдела нутрициологии биомедицинского холдинга «Атлас». — Он ошибался».

Важно понимать, что эктоморф, эндоморф и мезоморф — идеальные типы, которые почти не встречаются в чистом виде. «В действительности почти каждый человек представляет собой смесь типов телосложения, и большинство людей могут найти общие характеристики в одной из трех групп», — добавляет Гильман.

Нутрициолог также отмечает, что использовать типы фигуры как основу для составления диеты не стоит: «Для подавляющего большинства людей типирование тела создает больше вопросов, чем ответов. Оно делает питание неоправданно сложным, и это скорее отвлекает от тех принципов в питании, на которых важно фокусироваться».

Кроме того, стоит помнить, что параметры тела человека, количество жира и мышц у него определяют множество факторов и тип телосложения — не самый главный из них. Гораздо важнее образ жизни: количество физической активности, питание, вредные привычки и состояние здоровья.

Связанные вопросы и ответы:

Что такое фигура

фигуры, ж. (латин. figura – вид).

1. Внешнее очертание, вид, форма чего-н. (уар.). Фигура земли (мат., астр.).

2. В геометрии – часть плоскости, ограниченная замкнутой ломанной или кривой линией, а также вообще совокупность определенно расположенных точек, линий, поверхностей и тел (мат.). Геометрические фигуры (напр. треугольник, параллелограмм, конус и т.д.).

|| В книгах – название чертежа, схемы, рисунка (обычно пишется под изображением сокращенно: фиг.; тип.).

3. Положение, позиция, принимаемая кем-чем-н. при исполнении чего-н. в движении (в танце, фехтовании, катании на коньках, полете в воздухе и т. д.). Первая фигура кадрили. Фигуры высшего пилотажа.

4. Оборот речи, стилистический прием, усиливающий выразительность речи (лит.). Риторические фигуры. Фигура умолчания.

5. Скульптурное изображение человека или животного. Восковые фигуры. Лепные фигуры на фасаде здания.

|| В живописи – изображение человека или животного (живоп.).

6. Телосложение, внешнее очертание, формы человека. У нее стройная, удивительной силы и ловкости фигура. Лесков. Нескладная фигура. Статная фигура. Крупная фигура. стоит возле моей кровати та неподвижная фигура. Тургенев. Подозрительная фигура.

|| человек, как носитель каких-н. социальных или индивидуальных признаков и свойств. Велика фигура – человек с сильными чувствами, с огромными страстями? Гончаров….Середняк является у нас центральной фигурой земледелия. Сталин. Крупная политическая фигура.

|| Важное, значительное лицо, персона (разг. ирон.). В свое время он был фигурой.

8. В игральных картах – название старших карт (валет, дама, король, туз).

|| В шахматах – название старших шашек (король, ферзь, слон, конь, ладья), в отличие от пешек.

Какие основные типы фигур существуют

Окружность — это совокупность всех точек на плоскости, которые находятся на одинаковом расстоянии от заданной точки О , которая называется центром окружности .

Определение. Единичная окружность - окружность, радиус которой равен единице.

Определение. Круг - часть плоскости, ограничена окружностью.

Определение. Радиус окружности R - расстояние от центра окружности О до любой точки окружности.

Определение. Диаметр окружности D - отрезок, который соединяет две точки окружности и проходит через ее центр.

Основные свойства окружности

1. Диаметр окружности равен двум радиусам.

D = 2 r

2. Кратчайшее расстояние от центра окружности к секущей (хорде) всегда меньше радиуса.

3. Через три точки, которые не лежат на одной прямым, можно провести только одну окружность.

4. Среди всех замкнутых кривых с одинаковой длиной, окружность имеет наибольшую площадь.

5. Если две окружности соприкасаются в одной точке, то эта точка лежит на прямой, что проходит через центры этих окружностей.

Формулы длины окружности и площади круга

Формулы длины окружности

1. Формула длины окружности через диаметр:

L = π D

2. Формула длины окружности через радиус:

L = 2 πr

Уравнение окружности

Касательная окружности - прямая, которая касается окружности только в одной точке.

Основные свойства касательных к окружности

1. Касательная всегда перпендикулярна к радиусу окружности, проведенного в точке соприкосновения.

2. Кратчайшее расстояние от центра окружности к касательной равна радиусу окружности.

3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:

AB = AC

Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:

∠ОAС = ∠OAB

Секущая окружности и ее свойства

Определение. Секущая окружности - прямая, которая проходит через две точки окружности.

основные свойства секущих

1. если с точки вне окружности (q) выходят две секущие, которые пересекают окружность в двух точках a и b для одной секущей и c и d для другой секущей, то произведения отрезков двух секущих равны между собою:

AQ ∙ BQ = CQ ∙ DQ

2. Если из точки Q вне окружности выходит секущая прямая, что пересекает окружность в двух точках A и B, и касательная с точкой соприкосновения C, то произведение отрезков секущей равна квадрату длины отрезка касательной:

AQ ∙ BQ = CQ²

Хорда окружности ее длина и свойства

Определение. Хорда окружности - отрезок, который соединяет две точки окружности.

Основные свойства хорд

1. Две одинаковые хорды стягивают две одинаковые дуги:

если хорды AB = CD, то

дуги ◡ AB = ◡ CD

2. Если хорды параллельные, то дуги между ними будут одинаковые:

если хорды AB ∣∣ CD, то

◡ AD = ◡ BC

3. Если радиус окружности перпендикулярен к хорде, то он разделяет хорду пополам в точке их пересечения:

если OD ┴ AB, то

AC = BC

4. Если две хорды AB и CD пересекаются в точке Q, то произведение отрезков, что образовались при пересечении, одной хорды равны произведению отрезков другой хорды:

AQ ∙ BQ = DQ ∙ QC

5. Хорды с одинаковой длиной находятся на одинаковом расстоянии от центра окружности.

если хорды AB = CD, то

ON = OK

6. Чем больше хорда, тем ближе она к центру.

Каковы отличительные особенности круга

Вдля того, чтобы четырёхугольник был прямоугольником, достаточно, чтобы хотя бы три его угла были прямые, тогда четвёртый угол в силутакже будет равен 90°.

В геометрии доказывается, что две прямые,одной и той же третьей прямой, параллельны между собой. Применив эту теорему к противоположным сторонам прямоугольника, перпендикулярным смежным с ними сторонам, получаем, что противоположные стороны прямоугольника параллельны, поэтому каждый прямоугольник является.

В, где сумма углов четырёхугольника не равна 360°, прямоугольников в указанном приведённым определением смысле не существует, однако можно определить их обобщения .

Каковы отличительные особенности прямоугольника

С нами работают 108 689 преподавателей из 185 областей знаний. Мы публикуем только качественные материалы

Как работает сервис?

Понятие многоугольника

Определение 1

Многоугольником называется геометрическая фигура в плоскости, которая состоит из попарно соединенных между собой отрезков, соседние из которых не лежат на одной прямой.

При этом отрезки называются сторонами многоугольника , а их концы - вершинами многоугольника .

Определение 2

$n$-угольником называется многоугольник, у которого $n$ вершин.

Виды многоугольников

Определение 3

Если многоугольник всегда будет лежать по одну сторону от любой прямой, проходящей через его стороны, то многоугольник называется выпуклым (рис. 1).

Рисунок 1. Выпуклый многоугольник

Определение 4

Если многоугольник лежит по разные стороны хотя бы одной прямой, проходящей через его стороны, то многоугольник называется невыпуклым (рис. 2).

Рисунок 2. Невыпуклый многоугольник

Сумма углов многоугольника

Введем теорему о сумме углов -угольника.

Теорема 1

Сумма углов выпуклого -угольника определяется следующим образом

\

Доказательство.

Пусть нам дан выпуклый многоугольник $A_1A_2A_3A_4A_5\dots A_n$. Соединим его вершину $A_1$ со всеми другими вершинами данного многоугольника (рис. 3).

Рисунок 3.

При таком соединении мы получим $n-2$ треугольника. Просуммировав их углы мы получим сумму углов данного -угольника. Так как сумма углов треугольника равняется ${180}^0,$ получим, что сумма углов выпуклого -угольника определяется по формуле

\

Теорема доказана.

«Многоугольник, выпуклый многоугольник, четырехугольник»

Помощь эксперта по теме работы

Найти эксперта

Решение задач от ИИ за 2 минуты

Решить задачу

Помощь с рефератом от нейросети

Написать ИИ

Понятие четырехугольника

Используя определение $2$, легко ввести определение четырехугольника.

Определение 5

Четырехугольником называется многоугольник, у которого $4$ вершины (рис. 4).

Рисунок 4. Четырехугольник

Для четырехугольника аналогично определены понятия выпуклого четырехугольника и невыпуклого четырехугольника. Классическими примерами выпуклых четырехугольников являются квадрат, прямоугольник, трапеция, ромб, параллелограмм (рис. 5).

Рисунок 5. Выпуклые четырехугольники

Теорема 2

Сумма углов выпуклого четырехугольника равняется ${360}^0$

Доказательство.

По теореме $1$, мы знаем, что сумма углов выпуклого -угольника определяется по формуле

\

Следовательно, сумма углов выпуклого четырехугольника равняется

\

Теорема доказана.

Примеры задач

Пример 1

Определить сумму углов выпуклого девятиугольника, семиугольника и двенадцатиугольника.

Решение.

Для решения будем пользоваться теоремой $1$. Получим:

Сумма углов выпуклого пятиугольника равняется

\

Сумма углов выпуклого девятиугольника равняется

\

Сумма углов выпуклого двенадцатиугольника равняется

\

Пример 2

Сколько углов имеет выпуклый многоугольник, если сумма его углов равняется ${1620}^0$.

Решение.

Используя формулу задачи $1$, имеем

\ \ \

Ответ: $11$.

Каковы отличительные особенности треугольника

Садовникова О.П. 1

---

1 МОУ Лицей №10 им. Д. И. Менделеева

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке "Файлы работы" в формате PDF

Введение

Кривые с древних времен привлекали к себе внимание ученых и использовались ими для описания различных природных явлений от траектории брошенного камня до орбит космических тел. В школьном курсе математики в качестве кривых рассматриваются графики функций. На уроках математики я изучала параболу, гиперболу, окружность. Мне захотелось познакомиться с другими фигурами, населяющими удивительный мир математики, которые часто встречаются в нашей жизни. Одной из таких замечательных кривых является эллипс.

Актуальность темы . Я выбрала эту тему, так как считаю её интересной и увлекательной, открывающей практическое приложение математики в жизни. Кроме того, тема эллипс затрагивается при изучении темы «Конус» на уроках стереометрии.

Объектом исследования в моей работе является эллипс, а предметом исследования – характеристики эллипса, его свойства, их применение человеком в науке и технике.

Гипотеза. Знакомство с кривыми, изучение их свойств будет способствовать расширению геометрических представлений, позволит углубить знания, повысить интерес к геометрии, создаст содержательную основу для дальнейшего изучения математики, физики и др. наук.

Цель моей работы: изучить эллипс, совершенствуя тем самым уровень своей математической подготовки и расширяя свои знания по планиметрии. Я поставила перед собой следующие задачи: узнать, что такое эллипс; изучить свойства эллипса; научиться строить эллипс и касательную к нему с помощью циркуля и линейки; научиться решать задачи; рассмотреть практическую направленность свойств эллипса; обобщить найденный материал; выступить по данной теме на одном из уроков математики перед учащимися.

Практическая значимость. Я считаю, что использование данного материала на уроках математики позволит расширить кругозор учащихся, познакомит их с замечательными свойствами кривых, которые широко применяются в жизни. Также моя работа научит строить эллипс при помощи несложных школьных инструментов, продемонстрирует решение задач на нахождение элементов эллипса.

Методы исследования: научный (изучение литературы);исследовательский (анализ и обобщение материала); практический (выполнение построений).

2. Основная часть

2.1.Теоретическая часть

2.1.1. Каноническое уравнение эллипса.

Эллипс (от греч. « ellipsis » значит «недостаток» - возможно, имеется ввиду недостаток площади деформированной окружности) - этуфигуру знают все.Онабылаизвестна еще вДревней Греции . Еёоткрыл некий Менехм около 360 года до нашей эры, а до нас она дошли по сочинению выдающегося математика Аполлония, написанному примерно 200 лет спустя. С эллипсом встречаются в начальной астрономии и географии (траектории движения планет и спутников, форма земного меридиана, путь электрона вокруг ядра атома), в черчении, рисовании и стереометрии (рисунки технических деталей, круглых предметов и геометрических тел).

А как задать уравнение эллипса? Как с помощью формулы задать «приплюснутость» окружности?

Меня очень заинтересовал этот вопрос. Попробуем получить эллипс из окружности. Построим окружность. Через центр О окружности радиуса а проведем взаимно перпендикулярные диаметры А'А и D ' D . На радиусах О D , О D ' отложим от точки О равные отрезки ОВ, ОВ' длиной в (меньшей, чем а ). Из каждой точки N окружности опустим перпендикуляр NP на диаметр А'А и на этом перпендикуляре отложим от его основания Р отрезок РМ так, чтобы ( 1). Это построение преобразует каждую точку N в другую соответствующую ей точку М, лежащую на том же перпендикуляре N Р, причем РМ получается из Р N уменьшением в одном и том же отношении k .Такое преобразование называется равномерным сжатием. Прямая АА' называется осью сжатия. Линия АВА'В', в которую преобразуется окружность после равномерного сжатия, называется эллипсом. Точка О называется центром эллипса. Точки А, А', В, В' называются вершинами эллипса . Отношение k называется коэффициентом сжатия эллипса. Величина 1- k = (отношение) называется сжатием эллипса, оно обозначается буквой α . Окружность можно рассматривать как эллипс с коэффициентом сжатия k =1. Так земной меридиан точнее принять не за окружность, а за эллипс. Земная ось есть малая ось этого эллипса. Длина ее приближенно 12 712 км. Длина большой оси равна приближенно 12 754 км. Зная это, можно найти коэффициент сжатия k и сжатие α этого эллипса: k 0,997; ≈0,003 .

Каковы отличительные особенности многоугольника

С нами работают 108 689 преподавателей из 185 областей знаний. Мы публикуем только качественные материалы

Как работает сервис?

Понятие параллелепипеда

Определение 1

Геометрическая фигура, образованная двумя равными параллелограммами , лежащими в параллельных плоскостях , а их вершины соединены между собой так, что между параллельными плоскостями образуются две пары параллелограммов, лежащих в параллельных плоскостях , называется параллелепипедом (рис. 1).

Рисунок 1. Параллелепипед

Параллелограммы, из которых составлен параллелепипед, называются гранями параллелепипеда , стороны параллелограммов -- сторонами параллелепипеда , а вершины параллелограммов -- вершинами параллелепипеда .

Свойства параллелепипеда

Теорема 1

Противоположные грани параллелепипеда равны между собой и параллельны.

Доказательство.

Параллельность противоположных граней сразу исходит из определения 1.

Докажем равенство противоположных граней. Для этого рассмотрим рисунок 2.

Рисунок 2.

Рассмотрим грани ${AA}_1B_1B$ и ${DD}_1C_1C$. Так как, по определению 1, грани параллелепипеда -- параллелограммы, то ${AA}_1={DD}_1$ и $AB=DC.$ Так же ${AA}_1||{DD}_1$ и $AB||DC$, следовательно, $\overrightarrow{{AA}_1}\uparrow \uparrow \overrightarrow{{DD}_1}$ и $\overrightarrow{AB}\uparrow \uparrow \overrightarrow{DC}$, то есть $\angle A_1AB=\angle D_1DC$. Значит, по I признаку равенства треугольников $\triangle A_1AB=\triangle D_1DC$. Аналогично доказывается, что $\triangle D_1C_1C=\triangle A_1B_1B$, следовательно, $D_1C_1CD=A_1B_1BA$. Аналогично доказывается равенство других противоположных граней.

«Параллелепипед, сввойства прямоугольного параллелепипеда»

Помощь эксперта по теме работы

Найти эксперта

Решение задач от ИИ за 2 минуты

Решить задачу

Найди решение своей задачи среди 1 000 000 ответов

Найти

Теорема доказана.

Теорема 2

Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.

Доказательство.

Рассмотрим рисунок 3.

Рисунок 3.

Докажем вначале, что диагонали $A_1C$ и $D_1B$ делятся точкой пересечения $O$ пополам. По теореме 1, имеем $A_1D_1=BC$ и $A_1D_1||BC$. Следовательно, $A_1D_1CB$ -- параллелограмм. Тогда, по свойству параллелограмма, получим, что диагонали $A_1C$ и $D_1B$ делятся точкой пересечения $O$ пополам. Аналогично доказывается, что диагонали ${AC}_1$ и $D_1B$ и $A_1C$ и ${DB}_1$ делятся точками их пересечения пополам. Но, так как $O$ центр диагоналей $A_1C$ и $D_1B$, то все диагонали пересекаются в этой точке.

Теорема доказана.

Прямоугольный параллелепипед

Можно выделить два частных случая понятия параллелепипеда. Один из них -- понятие прямоугольного параллелепипеда.

Определение 2

Параллелепипед, у которого в основаниях лежат прямоугольники и все двугранные углы равны ${90}^0$ называется прямоугольным (рис. 4).

Прямоугольный параллелепипед">
Рисунок 4. Прямоугольный параллелепипед

Прямоугольный параллелепипед обладает теми же свойствами, что и произвольный, однако он помимо этого обладает отдельным свойством.

Теорема 3

Сумма квадратов трех измерений (высота, длина и ширина) равняется квадрату его диагонали.

Математически это можно записать следующим образом:

\

Рисунок 5.

Доказательство.

Рассмотрим рисунок 5. Докажем, для примера, что

Рассмотрим треугольник $ADC$. По теореме Пифагора, имеем

Так как $ABCD$ -- прямоугольник, то $DC=AB$, следовательно

Рассмотрим треугольник $ACC_1$. По теореме Пифагора, имеем

Так как ${CC}_1=AA_1$, то

Куб

Определение 3

Прямоугольный параллелепипед, гранями которого служат квадраты, называется кубом (рис. 6).

Рисунок 6.

Пример задачи

Пример 1

Найти длину диагонали куба, у которого высота равняется $3$.

Решение.

По определению куба, получим, что мы имеем прямоугольный параллелепипед, у которого и высота. И ширина и длина равны 3. Тогда, по теореме 3, имеем

\ \ \

Ответ: $3\sqrt{3}$.

Каковы отличительные особенности эллипса

План подготовки и проведения занятия:

I. Подготовительный этап:

1. Повторение известных свойств треугольной пирамиды.
2. Выдвижение гипотез о возможных, не рассмотренных ранее, особенностях тетраэдра.
3. Формирование групп для проведения исследований по данным гипотезам.
4. Распределение заданий для каждой группы (с учётом желания).
5. Распределение обязанностей по выполнению задания.

II. Основной этап:

1. Решение гипотезы.
2. Консультации с учителем.
3. Оформление работы.

III. Заключительный этап:

1. Представление и защита гипотезы.

Цели занятия:

• обобщить и систематизировать знания и умения учащихся; изучить дополнительный теоретический материал по указанной теме; научить применять знания при решении нестандартных задач, видеть в них простые составляющие;
• формировать навык работы учащихся с дополнительной литературой, совершенствовать умение анализировать, обобщать, находить главное в прочитанном, доказывать новое; развивать коммуникативные навыки учащихся;
• воспитывать графическую культуру.

Подготовительный этап (1урок):

1. Сообщение учащегося “Тайны великих пирамид”.
2. Вступительное слово учителя о разнообразии видов пирамид.
3. Обсуждение вопросов:

• По каким признакам можно объединять неправильные треугольные пирамиды
• Что мы понимаем под ортоцентром треугольника, и что можно называть ортоцентром тетраэдра
• Существует ли ортоцентр у прямоугольного тетраэдра
• Какой тетраэдр называют равногранным Какими свойствами он может обладать

1. В результате рассмотрения разнообразных тетраэдров, обсуждения их свойств уточняются понятия и появляется некоторая структура:

1. Рассмотрим свойства правильного тетраэдра .(Приложение)

Свойства 1-4 доказываются устно с использованием Слайда1.

Свойство 1: Все ребра равны.

Свойство 2: Все плоские углы равны 60°.

Свойство 3: Суммы плоских углов при любых трех вершинах тетраэдра равны 180°.

Свойство 4: Если тетраэдр правильный, то любая его вершина проектируется в ортоцентр противоположной грани.

Дано:

ABCD – правильный тетраэдр

AH – высота

Доказать:

H –ортоцентр

Доказательство:

1) точка H может совпадать с какой-либо из точек A, B, C. Пусть H ?B, H ?C

2) AH + (ABC) => AH + BH, AH + CH, AH + DH,

3) Рассмотрим ABH, BCH, ADH

AD – общая => ABH, BCH, ADH => BH =CH = DH

AB = AC = AD т. H – является ортоцентром ABC

Что и требовалось доказать.